[자료구조] 해시 테이블

Hash Table

개발하면서 또는 알고리즘 문제를 풀면서 해시 테이블을 이용해야하는 경우들이 있었을 것이다. 빠른 데이터 검색을 위해서 사용하는데, Java에서는 HashMap을 주로 사용한다.

특정한 키(key)에 대해서 해시 함수 또는 해시 알고리즘을 통해 일정한 길이의 해시(hash)를 만들어내고, 버킷(bucket)에 저장한다. 이후에 같은 키에 대해서 같은 해시를 만들어내고, 해시를 통해 해당 값(value)을 조회할 수 있다.

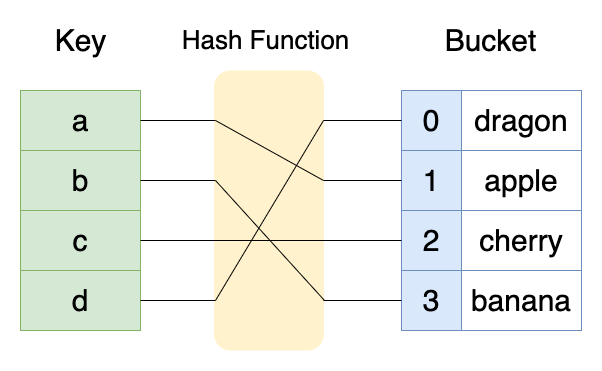
검색의 시간복잡도는 $ O(1) $ 이지만 해시 충돌(Hash Collision)로 인한 최악의 경우 $ O(N) $ 이 될 수도 있다.

Hash Collision

해시 충돌은 서로 다른 키에 대해서 같은 해시를 만들어내는 경우를 말한다.

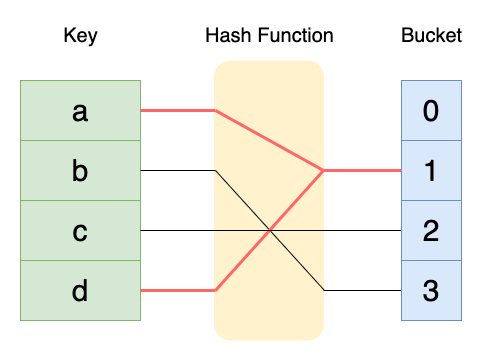
만약 위와 같이 키 a와 d에 대해서 같은 해시 값이 나올 때, 이를 해시 충돌이라 한다. 이러한 충돌을 해결하는 대표적인 방법으로 개방 주소법(Open Addressing)과 분리 연결법(Separate Chaining)이 있다.

Open Addressing

개방 주소법은 충돌 났을 때, 다른 비어있는 버킷을 찾는 방법이다. 비어있는 버킷을 찾을 때, 선형 탐색(Linear Probing), 제곱 탐색(Quadratic Probing), 이중 해시 등의 방법을 사용할 수 있다.

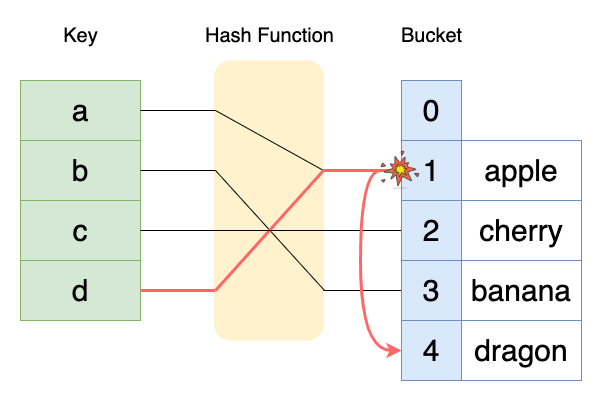
키 d에 대해서 충돌이 발생하자 비어있는 4번 버킷을 찾아 들어간다. 따라서 개방 주소법은 데이터의 주소값이 바뀌는 방식이다.

Separate Chaining

분리 연결법은 버킷에 값을 그대로 저장하는 것이 아니라, 버킷의 링크드리스트에 차곡차곡 저장한다. 뒤에서 설명하지만 반드시 링크드리스트는 아니고, 버킷에 값을 그대로 저장하지 않는 것에 집중하라.

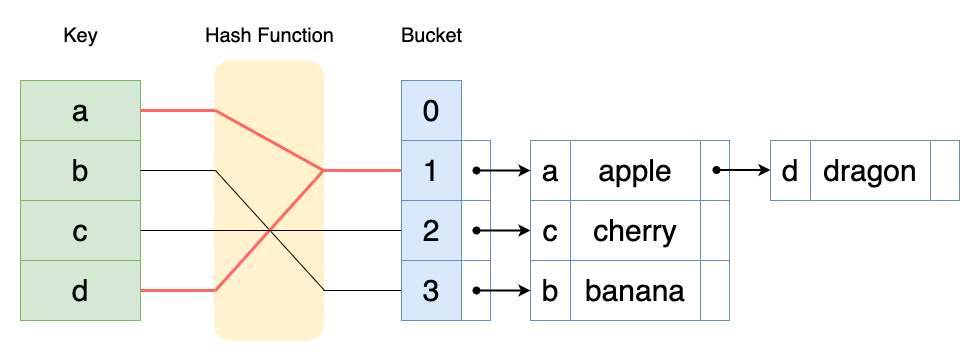
해시 충돌이 나더라도, 링크드리스트에 추가하는 방식으로 해결한다. 조회할 때에는 링크드리스트에서 키를 선형 탐색한다.

비교

두 방식의 비교는 네이버 D2 블로그에 좋은 글이 있어 그대로 가져왔다.

둘 모두 Worst Case O(M)이다. 하지만 Open Addressing은 연속된 공간에 데이터를 저장하기 때문에 Separate Chaining에 비하여 캐시 효율이 높다. 따라서 데이터 개수가 충분히 적다면 Open Addressing이 Separate Chaining보다 더 성능이 좋다. 하지만 배열의 크기가 커질수록(M 값이 커질수록) 캐시 효율이라는 Open Addressing의 장점은 사라진다. 배열의 크기가 커지면, L1, L2 캐시 적중률(hit ratio)이 낮아지기 때문이다.

Java HashMap에서 사용하는 방식은 Separate Channing이다. Open Addressing은 데이터를 삭제할 때 처리가 효율적이기 어려운데, HashMap에서 remove() 메서드는 매우 빈번하게 호출될 수 있기 때문이다. 게다가 HashMap에 저장된 키-값 쌍 개수가 일정 개수 이상으로 많아지면, 일반적으로 Open Addressing은 Separate Chaining보다 느리다. Open Addressing의 경우 해시 버킷을 채운 밀도가 높아질수록 Worst Case 발생 빈도가 더 높아지기 때문이다. 반면 Separate Chaining 방식의 경우 해시 충돌이 잘 발생하지 않도록 ‘조정’할 수 있다면 Worst Case 또는 Worst Case에 가까운 일이 발생하는 것을 줄일 수 있다. - 출처: https://d2.naver.com/helloworld/831311

Hash in Java

처음에도 언급했듯이, Java에서는 주로 HashMap을 사용한다.

Hashtable? HashMap?

Hashtable은 오래전에 사용되었던 클래스이고, HashMap 사용을 권장한다.

Hashtable은 thread-safe하고 HashMap은 thread-safe하지 않다는 차이가 있지만, 그렇다고 thread-safe를 위해서 Hashtable을 사용하지는 않고, ConcurrentHashMap를 사용하면 된다.

As of the Java 2 platform v1.2, this class was retrofitted to implement the Map interface, making it a member of the Java Collections Framework. Unlike the new collection implementations, Hashtable is synchronized. If a thread-safe implementation is not needed, it is recommended to use HashMap in place of Hashtable. If a thread-safe highly-concurrent implementation is desired, then it is recommended to use java.util.concurrent.ConcurrentHashMap in place of Hashtable. - 출처: Javadocs of Hashtable class

HashMap 자세히 들여다보기

본문은 JDK 11.0.2 기준으로 작성되었다.

`Node`

HashMap은 Separate Chaining방식을 선택했다. 버킷에는 노드가 저장되고 링크드리스트 형식으로 연결되어 저장될 것이다. HashMap에서 버킷(해시테이블)은 Node[]이며, Node는 다음 노드를 가리키는 next필드를 가지고 있다.

transient Node<K,V>[] table;

static class Node<K,V> implements Map.Entry<K,V> {
  final int hash;
  final K key;
  V value;
  Node<K,V> next;

  Node(int hash, K key, V value, Node<K,V> next) {
    this.hash = hash;
    this.key = key;
    this.value = value;
    this.next = next;
  }

  // 중략...
}

`put()`

하지만 더 자세히 들여다보면, Node 개수에 일정 이상이 되면 트리구조로 바뀌는 것을 알 수 있다. Node들이 충분히 커지면 TreeNode들로 변환되고, 이는 TreeMap과 유사한 구조를 가진다.(노드를 bin이라고 함)

This map usually acts as a binned (bucketed) hash table, but when bins get too large, they are transformed into bins of TreeNodes, each structured similarly to those in java.util.TreeMap. - 출처: Javadocs of HashMap

데이터가 많을 때에는 트리로 만듦으로써 더 빠른 get()을 보장한다.

아래 코드는 HashMap의 put()에 대한 코드인데, 24 번째 라인에서 binCount가 TREEIFY_THRESHOLD보다 커지면 트리 형식으로 바꾸는 것을 볼 수 있다. put() 뿐만 아니라 Node가 추가되는 상황에서 이러한 코드가 존재한다.

public V put(K key, V value) {
  return putVal(hash(key), key, value, false, true);
}

final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
              boolean evict) {
  Node<K,V>[] tab; Node<K,V> p; int n, i;
  if ((tab = table) == null || (n = tab.length) == 0)
    n = (tab = resize()).length;
  if ((p = tab[i = (n - 1) & hash]) == null)
    tab[i] = newNode(hash, key, value, null);
  else {
    Node<K,V> e; K k;
    if (p.hash == hash &&
      ((k = p.key) == key || (key != null && key.equals(k))))
      e = p;
    else if (p instanceof TreeNode)
      e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
    else {
      for (int binCount = 0; ; ++binCount) {
        if ((e = p.next) == null) {
          p.next = newNode(hash, key, value, null);
          if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
            treeifyBin(tab, hash);
          break;
        }
        if (e.hash == hash &&
          ((k = e.key) == key || (key != null && key.equals(k))))
          break;
        p = e;
      }
    }
    if (e != null) { // existing mapping for key
      V oldValue = e.value;
      if (!onlyIfAbsent || oldValue == null)
        e.value = value;
      afterNodeAccess(e);
      return oldValue;
    }
  }
  ++modCount;
  if (++size > threshold)
      resize();
  afterNodeInsertion(evict);
  return null;
}

노드 개수가 일정 이상 믾아져야 트리로 만드는 것은, 트리는 링크드리스트보다 메모리 사용량이 많고, 데이터의 개수가 적을 때 트리와 링크드리스트의 Worst Case 수행 시간 차이 비교는 의미가 없기 때문이다.

`TreeNode`

트리는 red-black 트리를 사용하는데 TreeMap과 거의 같다. 트리 순회 시 대소 판단 기준은 해시 값이다.

static final class TreeNode<K,V> extends LinkedHashMap.Entry<K,V> {
  TreeNode<K,V> parent;  // red-black tree links
  TreeNode<K,V> left;
  TreeNode<K,V> right;
  TreeNode<K,V> prev;    // needed to unlink next upon deletion
  boolean red;
  TreeNode(int hash, K key, V val, Node<K,V> next) {
      super(hash, key, val, next);
  }

  // 중략...
}

만약 직접 해시테이블을 만든다면?

해시 테이블을 만들기 위해서 적절한 해시 함수가 필요하다. 정해진 배열 크기 내에, 배치하기 위해 나머지 연산을 이용하면 좋다. 그에 따라 버킷의 크기는 소수(prime number)로 정하는 것이 좋다.

왜 소수여야 하는가

크기가 소수일 때와 그렇지 않을 때를 비교하면 바로 이해할 수 있다. 키(key)는 자연수만 온다고 가정하자. 단순 나머지 연산을 이용해 해시(인덱스)를 결정하고 해당 인덱스에 값을 채워보겠다.

가정 1: 버킷의 크기가 소수가 아닌 경우

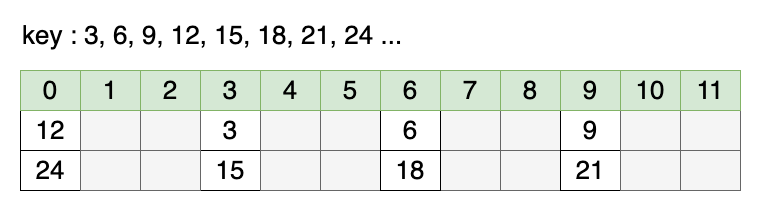
버킷의 크기는 12이고, 3의 배수들이 키(key)로 들어온다고 하면 위와 같다. 해시를 계산할 때 나머지 연산을 이용하며, 키를 버킷의 크기로 나눈 나머지 값(key % 12)을 이용한다. 이는 3이 12의 약수이기 때문에 발생하는 일로, 해시가 특정 값에 몰리고(해시 충돌), 다른 인덱스는 비어있음을 알 수 있다.

가정 2: 버킷의 크기가 소수인 경우

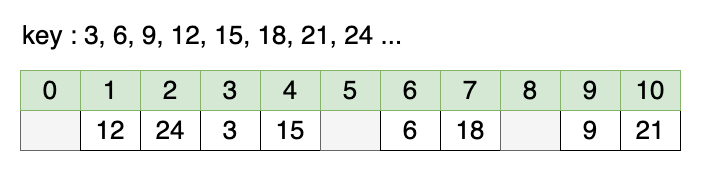
버킷의 크기는 11이고, 3의 배수들이 키(key)로 들어온다고 하면 위와 같다. 마찬가지로 키를 버킷의 크기로 나눈 나머지 값(key % 11)을 이용한다. 나머지 연산을 통해 인덱스를 결정하기 때문에, 버킷의 크기를 소수로 하면, 결과 값이 골고루 나오는 것을 알 수 있다. 나머지 연산에 의한 해시 충돌을 최대한 회피한다.

키가 문자열이라면

자연수에 대해서는 나머지 연산을 사용할 수 있지만, 문자열은 그럴 수 없다. 하지만 문자 역시 ASCII와 같은 숫자로 표현되므로 이를 이용한다. 실제로 java에서 String의 해시코드는 아래와 같이 계산한다.

// java.lang.String.hashCode()
public int hashCode() {
  int h = hash;
  if (h == 0 && value.length > 0) {
    hash = h = isLatin1() ? StringLatin1.hashCode(value)
                          : StringUTF16.hashCode(value);
  }
  return h;
}

// java.lang.StringLatin1.hashCode()
public static int hashCode(byte[] value) {
  int h = 0;
  for (byte v : value) {
    h = 31 * h + (v & 0xff);
  }
  return h;
}

위 코드를 식으로 풀면 아래와 같다.(내가 직접 알아낸건 아니고, hashCode() 위에 주석으로 쓰여져 있다) n은 문자열의 길이를 나타내며, 문자열 인덱스에 따라 31을 곱하면서 해시를 만들어낸다. 물론 해시가 커져서 int 범위를 넘어서면 오버플로우되면서 음수가 될 것이다

s[0]*31^(n-1) + s[1]*31^(n-2) + ... + s[n-1]

31을 사용하는 이유

String 객체 해시 함수에서 31을 사용하는 이유는, 31이 소수이며 또한 어떤 수에 31을 곱하는 것은 빠르게 계산할 수 있기 때문이다. 31N=32N-N인데, 32는 2의 5승 이니 어떤 수에 대한 32를 곱한 값은 shift 연산으로 쉽게 구현할 수 있다. 따라서 N에 31을 곱한 값은, (N « 5) – N과 같다. 31을 곱하는 연산은 이렇게 최적화된 머신 코드로 생성할 수 있기 때문에, String 클래스에서 해시 값을 계산할 때에는 31을 승수로 사용한다. - 출처: https://d2.naver.com/helloworld/831311

요약

해시 검색의 시간복잡도는 $O(1)$이지만 최악의 경우 $O(N)$이다.
해시 충돌에는 개방주소법(Open Addressing)과 분리연결법(Seperate Chaining)이 있다.
개방주소법은 다른 빈 버킷을 찾아 넣고, 분리연결법은 버킷을 링크드리스트로 만든다.
Java의 HashMap은 분리연결법을 사용하며, 노드 개수에 따라 링크드리스트이거나 레드블랙트리 구조를 가진다.
해시테이블을 만들 때, 키가 정수라면 나머지 연산을 활용하며 버킷의 크기는 소수로 하는 것이 좋다. 키가 문자열이라면 문자 데이터와 인덱스를 고려한다.