[프로그래머스] 정수삼각형 Java 풀이

PROBLEM

https://programmers.co.kr/learn/courses/30/lessons/43105

SOLUTION

DP를 이용하여, 바닥부터 탐색하며 최대값을 저장한다. 문제에서 제시하는 방향을 거꾸로 찾아가는 것이다. 예시를 보자.

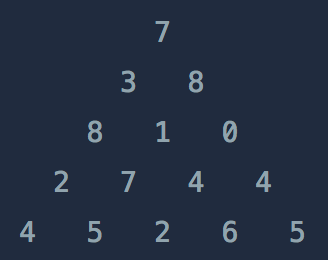
입출력예시

먼저 DP배열에는 바닥의 값으로 초기화시킨다.

dp 0 1 2 3 4
  4 5 2 6 5

다음, 바로 윗층에서 이동가능한 값 중 큰 값과 자신을 더한다. 7에서 이동가능한 곳은 5와 2이며 큰 값인 5를 취하여 최대 12를 만들 수 있다.

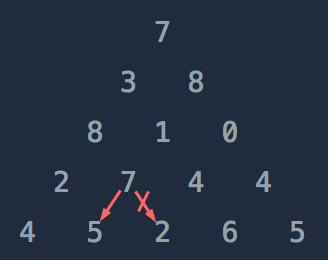
입출력예시4

[2, 7, 4, 4]를 각각 적용하면 아래와 같은 상태가 된다.

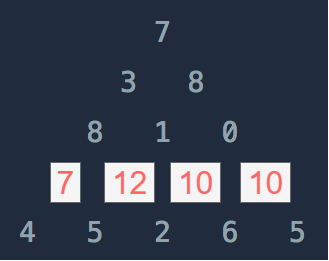
입출력예시2

DP배열에는 해당 값들을 저장한다. 이 때, 각 값들은 연산 과정에서 서로 영향을 미치지 않으므로 1차원 배열에 덮어써도 된다. DP배열에는 아래와 같이 저장되어 있겠지만, 맨 마지막 값인 5(dp[4])는 사용되지 않는다.

dp 0 1 2 3 4
  7 12 10 10 5

위와 같은 과정을 거치면 결국 아래와 같이 되므로 DP배열의 0 번째 요소인 30이 정답이다.

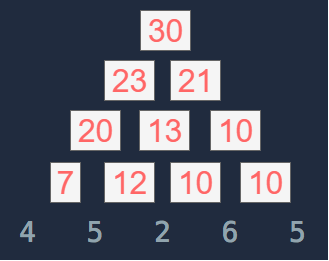
입출력예시3

dp 0 1 2 3 4
  30 21 10 10 5

SOURCE CODE (JAVA)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

class Solution {
  public int solution(int[][] triangle) {
    int answer = 0;

    int height = triangle.length - 1;
    int[] dp = new int[height + 1];

    // 초기값은 삼각형의 맨 밑층
    for (int i = 0; i <= height; i++)
      dp[i] = triangle[height][i];

    // 맨 밑층 부터 한 단계씩 올라가면서, 최선의 선택을 고른다.
    // 현 위치 (i-1, j)에서  선택할 수 있는 dp[j]와 dp[j-1]중 큰 값을 선택하고, 거기에 현재 값 triangle[i-1][j]을 더한게 최선의 선택이다.
    for (int i = height; i > 0; i--) {
      for (int j = 0; j < i; j++) {
        dp[j] = Math.max(dp[j], dp[j + 1]) + triangle[i - 1][j];
      }
    }

    // dp[0]에 (0,0)에서 선택할 수 있는 최선의 선택을 한 값이 저장되어 있다.
    answer = dp[0];

    return answer;
  }
}

댓글 남기기

관련있는 다른 게시글